最大回撤线性算法实现

发表于 2019-01-01 更新于 2023-05-05 分类于量化投资阅读次数：

最大回撤是指投资组合在选定的周期内，任一时间点往后推，可能出现资产净值下降的最大幅度。回撤的意思是指在某一段时期内净值从最高点开始回落到最低点的幅度。最大回撤常用百分率来表示，是一个重要的风险指标。最大回撤的计算公式为

$$
最大回撤 = \left( 波峰值 - 波谷值 \right) / 波峰值
$$

注意这里的$波峰值$与$波谷值$并不一定是最高值与最低值，这里的$波峰值$与$波谷值$要与时间范围内关联起来。

另外，值得指出的是，最大回撤只是描述投资组合资产净值下降的最大幅度，但它并没有描述投资组合需要使用多长时间恢复下降的资产净值。

本文讲述如何使用 Python 科学计算包 numpy 来计算最大回撤。

为方便描述算法，我们简化最大回撤的定义，只考虑净值下降值，不采用百分率来表示下降幅度，即对于序列 $x_1, x_2, \ldots, x_n$，定义最大回撤 $d$ 为

$$
d = \max \limits_{i\leqslant j} \left( x_i - x_j \right)
$$

如果需要改用百分率来表示最大回撤，只需要再除以$x_i$即可。

根据定义，很容易想到最大回撤的算法。遍历序列中所有元素，对于每个元素计算其下降最大值，然后再比较所有元素下降最大值，挑选出最大的元素下降最大值。这个算法的时间复杂度为$O(n^2)$。

那么，是否存在线性时间复杂度求最大回撤的算法呢？答案是肯定的。算法可以直接使用以下式子来表示：

$$
d = \max \limits_{i\leqslant j} \left( x_i - x_j \right) = \max \limits_{j} \left( \max \limits_{i \leqslant j} x_i - x_j \right)
$$

这个式子看着复杂，其实不难理解。式子左边是最大回撤的定义，上面我们介绍过了。下面介绍如何理解式子的右半部分。
我们先来看$\left( \max \limits_{i \leqslant j} x_i - x_j \right)$，假设我们指定元素$x_j$，元素$x_i$是指所有在元素$x_j$前的元素。$\max \limits_{i \leqslant j} x_i$ 表示所有在元素$x_j$前的元素中的最大元素，$\left( \max \limits_{i \leqslant j} x_i - x_j \right)$则表示这个最大元素减去元素$x_j$。说得或许还有点抽象，我们以一个具体例子来说明。
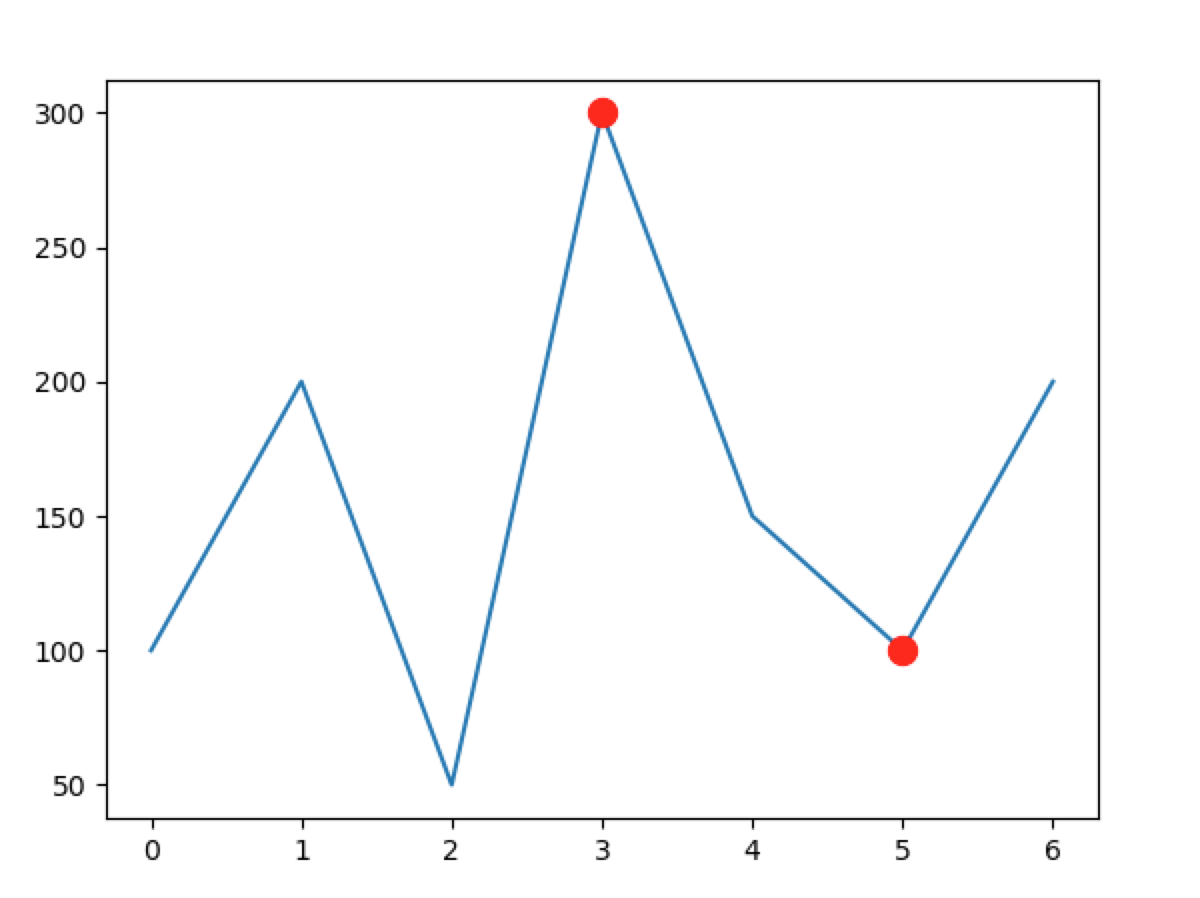
假设有一序列，[100, 200, 50, 300, 150, 100, 200]，元素下标以$0$来开始，指定$j$为4，$x_j$为150，则$i$可以取值 0, 1, 2, 3, 4，故 $\max \limits_{i \leqslant j} x_i$ 为 300，$\left( \max \limits_{i \leqslant j} x_i - x_j \right)$ 为 150。
现在再来看$\max \limits_{j} \left( \max \limits_{i \leqslant j} x_i - x_j \right)$来含义。前面我们可以计算到对于每个$j$，都有一个$\left( \max \limits_{i \leqslant j} x_i - x_j \right)$值，对于所有的$j$，取一个最大的$\left( \max \limits_{i \leqslant j} x_i - x_j \right)$值，即为最大回撤值，并取出取得最大回撤时对应的$j$和$i$下标，就完成算法的求解。

采用 Python 的 numpy 来实现这个算法，源代码如下：

import numpy as np
import matplotlib.pyplot as plt

x = [100, 200, 50, 300, 150, 100, 200]
j = np.argmax(np.maximum.accumulate(x) - x)
print('j is {j}'.format(j=j))
i = np.argmax(x[:j])
print('i is {i}'.format(i=i))
d = x[i] - x[j]
print(d)

plt.plot(x)
plt.plot([i, j], [x[i], x[j]],
         'o', color='Red', markersize=10)
plt.show()

为使用图形来展示最大回撤，我们使用了 matplotlib，输出结果：

j is 5
i is 3
200

输出的图形：

参考资料